This is a short introduction into compiled C code in Euler. Compiled code can be up to 100 times faster than Euler code. If you have existing C code, you may find it easy to implement this code for Euler.
Euler can load DLL (dynamic link library) files, and call the functions exported in these libraries. These libraries must be Windows DLLs from any compiler that can bind to a library. Some initialization is required, and the functions have a little overhead.
To make this easy, Euler comes with the Tiny C Compiler. See the following documentation about all details on this compiler.
Since this introduction is usually in a non-writable directory, we switch the current directory to the Euler directory in the home directory of the user.
>cd(eulerhome());
For an example, we implement the arithmetic geometric mean. The is is the limit of the sequence
![]()
This can be done in the language of EMT too. But it will be much faster in C.
The following function has the flag "tinyc" to tell the interpreter that this is C code. The number of parameters is read from the header as usual. The types of the parameters must be declared in the function body in C code. The result is returned by creating a new real on the Euler stack.
>function tinyc agm (a, b) ...
ARG_DOUBLE(a); ARG_DOUBLE(b);
CHECK(a>0 && b>0,"Need positive real numbers.");
double a1,b1;
while (1)
{
a1=(a+b)/2; b1=sqrt(a*b);
if (fabs(a1-b1)/a1<1e-14) break;
a=a1; b=b1;
if (test_key()) ERROR("User Interrupt!");
}
new_real(a1);
endfunction
As you see, the function has two ARG_DOUBLE macros. These macros define the double variables a and b, and assign the values of the arguments to these variables. Moreover, they check, if the user really entered two double arguments.
The loop does never fail by mathematical reasons. But to make sure, we check for a pressed key. The user can then interrupt the function with the escape key as usual.
The return value is put on the Euler stack in the proper format by the new_real() function.
>agm(2,10)
5.20801638106
The following is the Euler version of this function. It is typically slower by a factor of 10-50.
>function agmeuler (a:positive number, b:positive number) ...
repeat
{a,b}={(a+b)/2,sqrt(a*b)};
until a~=b;
end;
return a;
endfunction
>agmeuler(2,10)
5.20801638106
For a speed comparison, we need to do this a lot of times.
>tic; loop 1 to 100000; agm(2,10); end; toc,
Used 0.195 seconds 0.195
The algorithm in C should be around 10 times faster than in EMT.
>tic; loop 1 to 100000; agmeuler(2,10); end; toc,
Used 1.751 seconds 1.751
Here is an example, which benefits a lot from a little bit of C code. It computes the Hofstadter sequence, which is recursively defined by
![]()
We first implement this in EMT.
>function hofstadter (n) ...
v=ones(1,n);
loop 3 to n
k=v{#-1};
v{#}=v{k}+v{#-k};
end
return v
endfunction
The implementation in this function is about the fastest possible in Euler. We are using direct access to vector elements and a faster integer loop.
Here are the first 64 values.
>hofstadter(64)
[1, 1, 2, 2, 3, 4, 4, 4, 5, 6, 7, 7, 8, 8, 8, 8, 9, 10, 11, 12, 12, 13, 14, 14, 15, 15, 15, 16, 16, 16, 16, 16, 17, 18, 19, 20, 21, 21, 22, 23, 24, 24, 25, 26, 26, 27, 27, 27, 28, 29, 29, 30, 30, 30, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32]
It takes several seconds on my computer to compute about a million elements of the sequence.
>tic; v=hofstadter(2^20); toc;
Used 2.505 seconds
The following is a C function, which returns a matrix. The RES_ macro makes this easier for the user.
Once you execute the following definition, the following happens:
>function tinyc hofstadterfast (n) ...
## Computes n elements of the Hofstadter-Conway sequence.
ARG_INT(n);
CHECK(n>2,"Need an integer larger than 2.");
RES_DOUBLE_MATRIX(m,1,n);
m[0]=m[1]=1.0;
int i;
for (i=2; i<n; i++)
{
int k=(int)m[i-1];
m[i]=m[k-1]+m[i-k];
}
endfunction
The function seems to work.
>hofstadterfast(64)
[1, 1, 2, 2, 3, 4, 4, 4, 5, 6, 7, 7, 8, 8, 8, 8, 9, 10, 11, 12, 12, 13, 14, 14, 15, 15, 15, 16, 16, 16, 16, 16, 17, 18, 19, 20, 21, 21, 22, 23, 24, 24, 25, 26, 26, 27, 27, 27, 28, 29, 29, 30, 30, 30, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32]
And it is indeed much faster, typically by a factor of 100.
>tic; v=hofstadterfast(2^20); toc;
Used 0.009 seconds
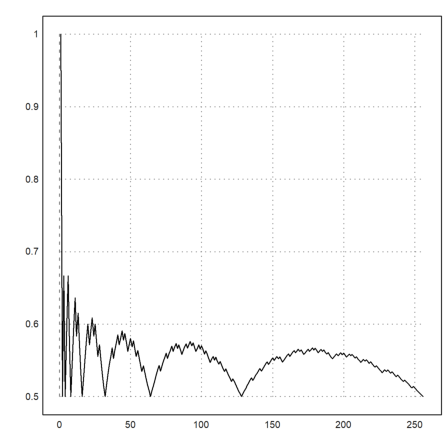
By the way, the sequence has an interesting behavior.
>i=1:256; plot2d(v[i]/i):
The help line in the definition is used for the status line and the help function. It will also be displayed in the help window. Try double clicking on the name of the function.
>help hofstadterfast
hofstadterfast is a comment function or a maxima function. function hofstadterfast (n) Entered from command line. Computes n elements of the Hofstadter-Conway sequence.
I have done the same example in Python. The speed of Python is in between EMT and C code, usually losing a factor of 5-10 to C code.
As a word of warning, vectorized Euler functions are more flexible and may be even faster than C functions.
As an example, we define a vectorized version of a simple function in C.
>cd(eulerhome()); function tinyc f(x) ...
ARG_DOUBLE_MATRIX(x,r,c);
RES_DOUBLE_MATRIX(y,r,c);
for (int i=0; i<r*c; i++)
{
*y=exp(-(*x)*(*x)/2)/sqrt(2*3.141592653589793);
y++; x++;
}
endfunction
The loop goes over all elements of the matrix x, storing the results in the matrix y.
>n=1000000; v=random(1,n); ... tic; f(v); toc;
Used 0.023 seconds
If we use a simple Euler function, we find that it is is on the same level.
>function feul (x) := exp(-x*x/2)/sqrt(2*pi); ... tic; feul(v); toc;
Used 0.029 seconds
So you should use vectorization, whenever possible. But it may sometimes require tricky commands. Often, the problem is easier solved by using fast C code.
For another example, we define a function, which switches two successive elements in a vector.
>function tinyc cswitch (v) ...
ARG_DOUBLE_MATRIX(x,r,c);
CHECK(r==1 && c%2==0,"Need a 1x2k vector");
RES_DOUBLE_MATRIX(y,r,c);
int i;
for (i=0; i<c; i+=2)
{
y[i]=x[i+1]; y[i+1]=x[i];
}
endfunction
>cswitch(1:10)
[2, 1, 4, 3, 6, 5, 8, 7, 10, 9]
To imitate this function in Euler using a loop is not a good idea.
Instead, there are various ways to make the matrix language work for this. One of them is to reorder the elements of v after they have been put in a matrix with two columns.
>function eswitch (v) ... n=cols(v); return redim(fliplr(redim(v,[n/2,2])),1,n); endfunction
>eswitch(1:10)
[2, 1, 4, 3, 6, 5, 8, 7, 10, 9]
Timing the two versions shows that the Euler function can compete.
>tic; cswitch(1:1000000); toc; ... tic; eswitch(1:1000000); toc;
Used 0.007 seconds Used 0.013 seconds
In many cases Tiny C functions are not sufficient. You need to write the complete C code, if
For an example, we define bitsets. The bitset is stored in binary data in Euler variables.
Since this tutorial is in a non-writable directory, we copy the souce code to the home directly of the user and compile it there.
>filecopy(home()+"bitsets.c",eulerhome()+"bitsets.c"); ... cd(eulerhome()); tccompile bitsets
If we have compiled our own DLL, we need to load the functions from the DLL one by one.
It is clear that the following command are best kept in an Euler file. Especially considering that a DLL can crash if a function is called with the false number of arguments.
>dll("bitsets","bmake",1); ...
dll("bitsets","bset",2); ...
dll("bitsets","bget",1); ...
dll("bitsets","band",2); ...
dll("bitsets","bor",2); ...
dll("bitsets","bsieve",1); ...
dll("bitsets","bfactor",2);
The Euler file could contain comment functions, which are non-callable functions to provide a help line.
>function comment bmake (n) ... ## Makes a bitset of size n. endfunction
Let us try the function and generate a bit set for 260 bits.
>bs=bmake(260)
Binary data of 37 bytes
We set all bits at prime indices to 1. Note that the bitset does not contain bit number 0.
>bset(bs,nonzeros(isprime(1:260)))
Also, note that the bitset has been changed. Arguments to DLL functions are by reference.
>bget(bs)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257]
If we wish to create a bitset and set the bits automatically, we can easily write a function for this.
Note that bset(w,v) is not returning the bitset. It sets the bits of w, changing this variable.
>function bits (v) ... ## A bitset, where the bits with indices in v are set. w=bmake(max(v)); bset(w,v); return w; endfunction
>bq=bits((1:16)^2+1);
Now we can call the operator band() to return all bits, which are set in both bitsets. This function does return a bitset.
>bget(band(bs,bq))
[2, 5, 17, 37, 101, 197, 257]
Or we can return a bitset with all bits set in one of the bitsets.
>bget(bor(bits([10,1,4,5]),bits([4,5,6])))
[1, 4, 5, 6, 10]
Using bget, we can extract the bits, which are set.
The DLL does also contain the sieve of Eratosthenes. It stores only odd numbers. So with 10 MB we can generate all primes up to 160 millions.
>n=80000000; pr=bsieve(n)
Binary data of 10000005 bytes
The number of primes found is about 9 millions.
>length(bget(pr))
8974457
Here is a function, which returns all primes up to n. Remember, that we only store the odd numbers 3,5,7,...
>function bprimes(n) := 1|(bget(bsieve(n))*2+1); >bprimes(100)
[1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199]
The bitsets file contains a factorization. The maximal integer, which can be represented exactly in double precision has 16 digits. So we need only the primes up to 10^8.
These are 500 million numbers. My computer takes some seconds to compute them.
>tic; pr=bsieve(10^8/2); toc;
Used 0.278 seconds
But now we can factor all possible integers, which can be stored in the double format.
>bfactor(1234283487123477,pr), longest prod(%)
[3, 7, 839, 1289, 1669, 32563]
1234283487123477
Here is a 15 digit prime number.
>longest bfactor(123456789012419,pr)
123456789012419
Due to good matrix programming, the sieve in Euler is not much slower. But it cannot handle that many primes.
We can generate the primes up to 40 million before we get an overflow in the heap.
>long length(primes(40000000))
2433654
It is possible to call an Euler function from C. The interface has an initialization routine, which passes pointers to several functions in Euler. One of them is a function, which interprets Euler functions.
For a very simple example, we define the bisection method for the solution of y=f(x), where f is a function in Euler. For simplicity, we assume f(a)>0 and f(b)<0.
The calling C functions must put all parameters as Euler headers to the stack at position h, call the function, and evaluate the result, which it finds at the stack at position h. It should check the state of the error flag.
>cd(eulerhome()); function tinyc cbisect (f,a,b) ...
ARG_STRING(f);
ARG_DOUBLE(a);
ARG_DOUBLE(b);
double m;
while (b-a>1e-15)
{
m=(a+b)/2;
header *h=new_real(m);
EVAL(f,h); IFERROR("Error in evaluation of f(m)");
if (*realof(h)>0) a=m;
else b=m;
}
new_real(m);
endfunction
>function f(x) := cos(x)-x; ...
cbisect("f",0,1), solve("cos(x)-x",1)
0.739085133215 0.739085133215
Here are some more examples.