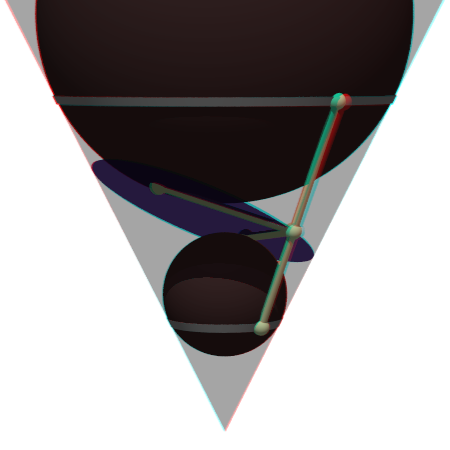
You can run this demonstration, if you have Povray installed, and pvengine.exe in the program path. Save the notebook to to your Euler Files first.
First we compute the radii of the spheres.
If you look at the figure below, you see that we need two circles touching the two lines which form the cone, and one line which forms the plane cutting the cone.
We use the geometry file of Euler for this.
>load geometry;
First the two lines forming the cone.
>g1 &= lineThrough([0,0],[1,a])
[- a, 1, 0]
>g2 &= lineThrough([0,0],[-1,a])
[- a, - 1, 0]
Thenm a third line.
>g &= lineThrough([-1,0],[1,1])
[- 1, 2, 1]
We plot everything so far.
>setPlotRange(-1,1,0,2); >color(black); plotLine(g(),"") >a:=2; color(blue); plotLine(g1(),""), plotLine(g2(),""):
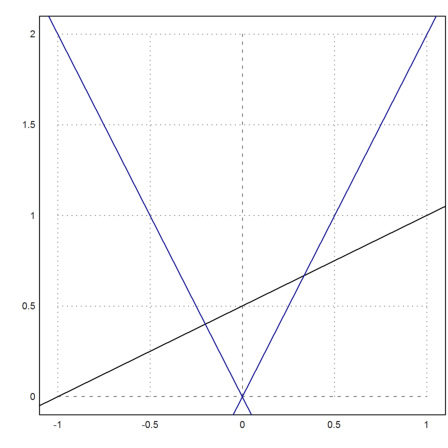
Now we take a general point on the y-axis.
>P &= [0,u]
[0, u]
Compute the distance to g1.
>d1 &= distance(P,projectToLine(P,g1))
2 2 2
a u 2 a u
sqrt((------ - u) + ---------)
2 2 2
a + 1 (a + 1)
Compute the distance to g.
>d &= distance(P,projectToLine(P,g))
2
u + 2 2 (2 u - 1)
sqrt((----- - u) + ----------)
5 25
And find the centers of the two circles, where the distances are equal.
>sol &= solve(d1^2=d^2,u)
2 2
- sqrt(5) sqrt(a + 1) + 2 a + 2
[u = ---------------------------------,
2
4 a - 1
2 2
sqrt(5) sqrt(a + 1) + 2 a + 2
u = -------------------------------]
2
4 a - 1
There are two solutions.
We evaluate the symbolic solutions, and find both centers, and both distances.
>u := sol()
[0.333333, 1]
>dd := d()
[0.149071, 0.447214]
Plot the circles into the figure.
>color(red); >plotCircle(circleWithCenter([0,u[1]],dd[1]),""); >plotCircle(circleWithCenter([0,u[2]],dd[2]),""); >insimg;
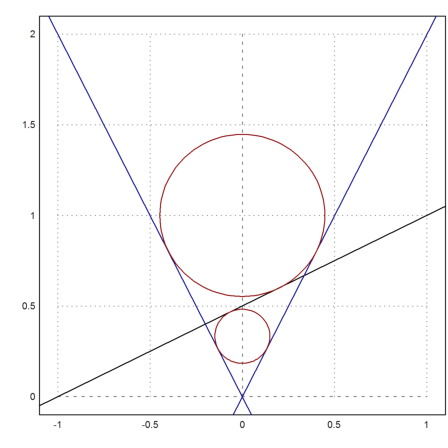
Next we plot everything with Povray. Note that you change any command in the following sequence of Povray commands, and rerun all commands with Shift-Return.
First we load the povray functions.
>load povray;
We setup the scene appropriately.
>povstart(zoom=11,center=[0,0,0.5],height=10°,angle=140°);
Next we write the two spheres to the Povray file.
>writeln(povsphere([0,0,u[1]],dd[1],povlook(red))); >writeln(povsphere([0,0,u[2]],dd[2],povlook(red)));
And the cone, transparent.
>writeln(povcone([0,0,0],0,[0,0,a],1,povlook(lightgray,1)));
We generate a plane restricted to the cone.
>gp=g(); >pc=povcone([0,0,0],0,[0,0,a],1,""); >vp=[gp[1],0,gp[2]]; dp=gp[3]; >writeln(povplane(vp,dp,povlook(blue,0.5),pc));
Now we generate two points on the circles, where the spheres touch the cone.
>function turnz(v) := return [-v[2],v[1],v[3]] >P1=projectToLine([0,u[1]],g1()); P1=turnz([P1[1],0,P1[2]]); >writeln(povpoint(P1,povlook(yellow))); >P2=projectToLine([0,u[2]],g1()); P2=turnz([P2[1],0,P2[2]]); >writeln(povpoint(P2,povlook(yellow)));
Then we generate the two points where the spheres touch the plane. These are the foci of the ellipse.
>P3=projectToLine([0,u[1]],g()); P3=[P3[1],0,P3[2]]; >writeln(povpoint(P3,povlook(yellow))); >P4=projectToLine([0,u[2]],g()); P4=[P4[1],0,P4[2]]; >writeln(povpoint(P4,povlook(yellow)));
Next we compute the intersection of P1P2 with the plane.
>t1=scalp(vp,P1)-dp; t2=scalp(vp,P2)-dp; P5=P1+t1/(t1-t2)*(P2-P1); >writeln(povpoint(P5,povlook(yellow)));
We connect the points with line segments.
>writeln(povsegment(P1,P2,povlook(yellow))); >writeln(povsegment(P5,P3,povlook(yellow))); >writeln(povsegment(P5,P4,povlook(yellow)));
Now we generate a gray band, where the spheres touch the cone.
>pcw=povcone([0,0,0],0,[0,0,a],1.01); >pc1=povcylinder([0,0,P1[3]-defaultpointsize/2],[0,0,P1[3]+defaultpointsize/2],1); >writeln(povintersection([pcw,pc1],povlook(gray))); >pc2=povcylinder([0,0,P2[3]-defaultpointsize/2],[0,0,P2[3]+defaultpointsize/2],1); >writeln(povintersection([pcw,pc2],povlook(gray)));
End the file, and start the Povray program.
>povend();
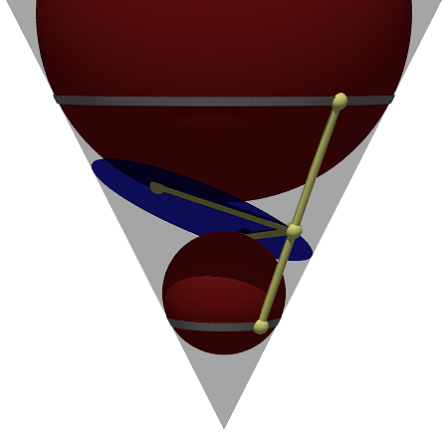
To get an Anaglyph of this we need to put everything into a scene function. This function will be used twice later.
>function scene () ... global a,u,dd,g,g1,defaultpointsize; writeln(povsphere([0,0,u[1]],dd[1],povlook(red))); writeln(povsphere([0,0,u[2]],dd[2],povlook(red))); writeln(povcone([0,0,0],0,[0,0,a],1,povlook(lightgray,1))); gp=g(); pc=povcone([0,0,0],0,[0,0,a],1,""); vp=[gp[1],0,gp[2]]; dp=gp[3]; writeln(povplane(vp,dp,povlook(blue,0.5),pc)); P1=projectToLine([0,u[1]],g1()); P1=turnz([P1[1],0,P1[2]]); writeln(povpoint(P1,povlook(yellow))); P2=projectToLine([0,u[2]],g1()); P2=turnz([P2[1],0,P2[2]]); writeln(povpoint(P2,povlook(yellow))); P3=projectToLine([0,u[1]],g()); P3=[P3[1],0,P3[2]]; writeln(povpoint(P3,povlook(yellow))); P4=projectToLine([0,u[2]],g()); P4=[P4[1],0,P4[2]]; writeln(povpoint(P4,povlook(yellow))); t1=scalp(vp,P1)-dp; t2=scalp(vp,P2)-dp; P5=P1+t1/(t1-t2)*(P2-P1); writeln(povpoint(P5,povlook(yellow))); writeln(povsegment(P1,P2,povlook(yellow))); writeln(povsegment(P5,P3,povlook(yellow))); writeln(povsegment(P5,P4,povlook(yellow))); pcw=povcone([0,0,0],0,[0,0,a],1.01); pc1=povcylinder([0,0,P1[3]-defaultpointsize/2],[0,0,P1[3]+defaultpointsize/2],1); writeln(povintersection([pcw,pc1],povlook(gray))); pc2=povcylinder([0,0,P2[3]-defaultpointsize/2],[0,0,P2[3]+defaultpointsize/2],1); writeln(povintersection([pcw,pc2],povlook(gray))); endfunction
You need red/cyan glasses to appreciate the following effect.
>povanaglyph("scene",zoom=11,center=[0,0,0.5],height=10°,angle=140°);